Ising Model

by John Doe, Feb 17, 2026

The Ising model is perhaps the most prevalent statistical model in physics, serving as the “fruit fly” for understanding phase transitions, critical phenomena, and emergent behavior in complex systems. While deceptively simple in its definition, it successfully reproduces the collective behavior observed in real-world ferromagnetic materials.

This post presents the results of a computational study of the 2D Ising model, moving from the microscopic dynamics of individual spins to macroscopic thermodynamic observables.

Mathematical Foundations

The model is defined on a graph $G (V, E)$ , where each vertex $i$ hosts a discrete spin variable $σ_{i} \in {- 1, + 1}$ (representing “down” or “up” magnetic moments). The energy of a specific configuration of spins is given by the Hamiltonian:

H ({σ}) = - J \sum_{⟨ i, j ⟩ \in E} σ_{i} σ_{j} - h \sum_{i} σ_{i}

Where $⟨ i, j ⟩$ denotes summation over nearest-neighbor pairs connected by edges.

$J$ is the coupling constant. We consider the ferromagnetic case where $J > 0$ , meaning neighboring spins lower their energy by aligning ( $σ_{i} = σ_{j}$ ).
$h$ is an external magnetic field. For this study, we set $h = 0$ to observe spontaneous symmetry breaking.

We are interested in how the macroscopic order of the system changes with temperature $T$ , governed by the Boltzmann distribution probability $P ({σ}) \propto e^{- H / k_{B} T}$ . The key macroscopic observables we calculate are:

Magnetization (Order Parameter): $M = \frac{1}{N} \sum_{i} σ_{i}$ . We look at $⟨ | M | ⟩$ to quantify the degree of order regardless of direction.
Magnetic Susceptibility ( $χ$ ): Related to fluctuations in magnetization. $χ = \frac{N}{k_{B} T} (⟨ M^{2} ⟩ - ⟨ M ⟩^{2})$
Specific Heat ( $C_{v}$ ): Related to fluctuations in internal energy. $C_{v} = \frac{N}{k_{B} T^{2}} (⟨ H^{2} ⟩ - ⟨ H ⟩^{2})$

Simulation Methodology

To simulate thermal equilibrium, we employ Markov Chain Monte Carlo (MCMC) methods, specifically the single-spin-flip Metropolis-Hastings algorithm.

For each step, we propose flipping a random spin $σ_{i} \to - σ_{i}$ and calculate the resulting change in energy, $Δ E$ . The flip is accepted with probability:

P_{a c c} = min (1, e^{- Δ E / k_{B} T})

This satisfies detailed balance, ensuring the system eventually reaches the Boltzmann equilibrium distribution. To handle significant computational loads, the underlying graph topology (a 2D periodic lattice) was represented using SciPy sparse matrices, and the core Metropolis loop was JIT-compiled using Numba to achieve near C-level performance.

Discussion of Results

The following dashboard summarizes the complete analysis, visualizing the system from four different analytical perspectives.

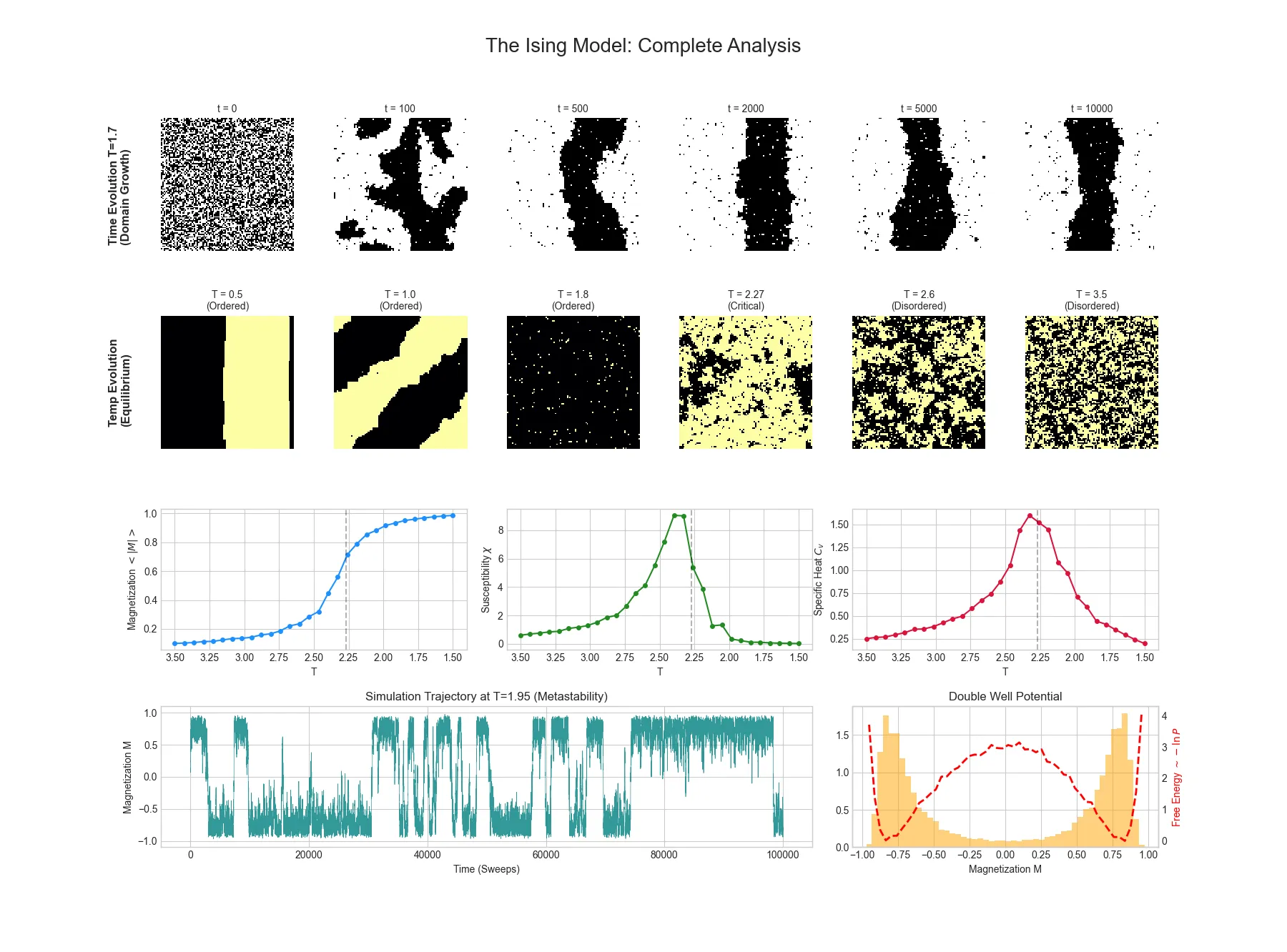
1. Microscopic Dynamics and Domain Growth

The top row visualizes the non-equilibrium time evolution of the lattice at a fixed temperature below the critical point ( $T = 1.7 < T_{c}$ ). At $t = 0$ , the system is initialized as a random paramagnetic state (infinite temperature). As the simulation proceeds, thermal noise is insufficient to overcome the ferromagnetic ordering tendency. We observe the nucleation of small ordered clusters, which subsequently grow and merge. This process, known as coarsening or domain growth, shows the system striving to minimize interfacial energy by reducing the boundary length between “up” and “down” regions, eventually approaching a uniform ordered state.

2. Macroscopic Equilibrium States

The second row displays equilibrium snapshots of the lattice across a range of temperatures.

Low Temperature ( $T = 0.5, 1.0$ ): The system is deeply in the ordered ferromagnetic phase. Note at $T = 0.5$ , a stable “domain wall” exists; the thermal energy is too low to allow the system to escape this local energy minimum and align fully.
High Temperature ( $T = 2.6, 3.5$ ): Entropy dominates. The system is in the disordered paramagnetic phase, resembling random noise.
Critical Temperature ( $T \approx 2.27$ ): The system exhibits critical opalescence. We observe fractal-like clusters of spins at all length scales, indicating the divergence of the correlation length.

3. Quantitative Phase Transition

The third row presents the thermodynamic averages plotted against temperature, confirming the visual intuition from the snapshots.

Magnetization: Shows a sharp, continuous phase transition. Below critical temperature $T_{c}$ , spontaneous symmetry breaking occurs, and $⟨ | M | ⟩$ rapidly rises from 0 toward 1.
Susceptibility & Specific Heat: Both quantities exhibit sharp peaks (theoretically diverging in the infinite size limit) precisely at the critical temperature. This indicates that at $T_{c}$ , the system becomes hypersensitive to external perturbations and experiences maximum fluctuations in energy and magnetic order.

4. Metastability and the Free Energy Landscape

The final row investigates the system’s behavior at a temperature slightly below critical ( $T = 1.95$ ), where thermal fluctuations are significant but order prevails.

Trajectory (Left): The time series of magnetization shows the system residing in stable states near $M \approx \pm 0.9$ . Crucially, it shows spontaneous “tunneling” events where rare, large thermal fluctuations kick the entire system over the energy barrier from one state to the other.
Free Energy Potential (Right): By histogramming the trajectory to get an empirical probability distribution $P (M)$ , we reconstruct the underlying effective free energy landscape $F (M) \sim - k_{B} T \ln P (M)$ . The result is a classic symmetric double-well potential. The two minima correspond to the stable ferromagnetic states, and the central hump at $M = 0$ represents the unstable energy barrier that necessitates symmetry breaking.